 One of the most important concepts in corporate finance is the time value of money. This concept is crucial in areas like capital budgeting, lease-or-buy decisions, accounts receivable analysis and many others. The time value of money is the relationship between $1 now and $1 at some time in the future.
One of the most important concepts in corporate finance is the time value of money. This concept is crucial in areas like capital budgeting, lease-or-buy decisions, accounts receivable analysis and many others. The time value of money is the relationship between $1 now and $1 at some time in the future.
We can illustrate the time value of money with an example. Imagine someone offered you $1000 as a gift. They said you could either have the $1000 right now, or you could have the money in 10 years from now. Which would you choose? Most rational people would choose to get the money now. This is because if you get $1000 now, you can make use of the money right away (to buy things, invest it, etc.) rather than wait. Additionally, who knows what the state of the world will be in 10 years, the dollar may have depreciated or even worse, the world may have ended. Clearly, receiving $1000 now is more valuable to most people than receiving $1000 in the future. In summary, benefits are foregone by waiting for money.
The time value of money is why “rational” people who lend money, require something more than just the principal to be repaid. The longer the lender has to wait for repayment and the riskier the loan, the more they require in return.
This means that dollar amounts received at different points in time must be converted to their values at a common date so that the amounts can be compared. To compare amounts at different time periods we introduce the two fundamental time value of money concepts: future value and present value.
Future Value
Because of the time value of money, it’s better to have money now rather than some time in the future. Think about the difference between having $100.00 now and $100.00 in one year from now. If you have $100 now, you can invest it in a savings account that earns, let’s say, 5% interest per year. This means that at after one year, you will have $105.00. The $105.00 is what is called the future value of $100.00 in one year when the rate of return is 5%.
Multiple Periods
For multiple years (or time periods), interest is compounded which means that interest is calculated on interest. Therefore, after two years at an interest rate of 5%, the future value of $100 is:
$100.00 x 1.05 x 1.05 = $110.25
To summarize, future value is the amount a present some of money will be, given a specified time period and interest rate.
For those who are mathematically inclined, here is the general formula to calculate future value:
FutureValue = PresentValue x (1 + InterestRate)NumberOfPeriods
Present Value
In order for investors to compare future cash inflows, it’s convenient to determine the value of money received in the future to its value today.
For example, suppose you need to accumulate $100,000 over 10 years for your child’s education. You happen to have cash available to make an investment that returns 7% per year. How much would you need to invest now in order to have $100,000 in 10 years? This amount represents the present value of $100,000 in 10 years at a 7% interest rate. To find present values, we can rearrange the future value formula above to show that:
PresentValue = FutureValue / (1 + InterestRate)NumberOfPeriods
For our exampe:
Present Value = $100,000 / (1 + 1.07)10 = $50,834.93
This means that at a rate of return of 7%, you would have to invest $50,834.93 for 10 years to accumulate $100,000.
Net Present Value (NPV)
Net Present Value or NPV for short, is another key concept for making financial decisions. Should you go ahead with that project? Should you buy that machine? NPV builds builds upon the idea of present value by including the current cost of an activity or investment, rather than just calculating the returns of the activity or investment. Simply put, the present value of all costs are calculated and compared with the present value of all future returns. The investment deciscion is then based on comparing these numbers.
NPV = Present value of investment returns – Present value of investment costs
As a rule, an investment is worth making if it has a positive NPV. The investment should be rejected if it has a negative NPV.
Annuities
In many cases, cash from investments is received at over time at regular intervals. Retirement pensions, leases, mortgages and pension plans are all annuities.
Calculating present and future values of annuities is also possible but a bit more complicated.
Financial Calculators Make Life Easier
Many calculators for calculating present values, future values and annuities are available. An easy to use financial calculator is available on our Free Financial Calculator page.
 Let’s say you’re trying to decide whether or not to produce a certain product. Say a new type of cuddly teddy bear. You’ll inevitably ask yourself “how many teddy bears do I need to sell to break even?” Breakeven analysis helps you answer that question.
Let’s say you’re trying to decide whether or not to produce a certain product. Say a new type of cuddly teddy bear. You’ll inevitably ask yourself “how many teddy bears do I need to sell to break even?” Breakeven analysis helps you answer that question. Computing and interpreting financial ratios is the cornerstone of financial statement analysis. The main financial statements are the
Computing and interpreting financial ratios is the cornerstone of financial statement analysis. The main financial statements are the  As discussed in another article, the
As discussed in another article, the 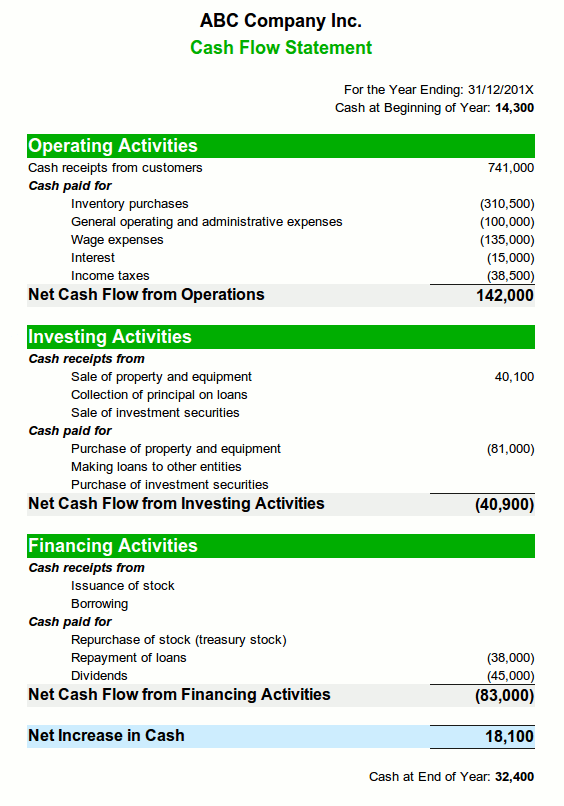
 The economic performance of an organization over a period of time is reported by an income statement. It reports all revenues and expenses over a specific time period. This differs from the
The economic performance of an organization over a period of time is reported by an income statement. It reports all revenues and expenses over a specific time period. This differs from the 
 One of the main financial statements used by decision makers in an organization is the balance sheet. The balance sheet shows the financial status of an organization at a specific point in time. It’s a “snapshot” of how the firm is doing. It also referred to as the statement of financial position or the statement of financial condition
One of the main financial statements used by decision makers in an organization is the balance sheet. The balance sheet shows the financial status of an organization at a specific point in time. It’s a “snapshot” of how the firm is doing. It also referred to as the statement of financial position or the statement of financial condition
 Organizations have financial goals. Accountants use available data to measure the results of the activities of an organization. The results are then reported to help decision makers measure financial success. Accounting information is helpful to those responsible for making decisions about the activities of an organization. Business owners, managers, investors as well as politicians are all examples of this type of decision maker.
Organizations have financial goals. Accountants use available data to measure the results of the activities of an organization. The results are then reported to help decision makers measure financial success. Accounting information is helpful to those responsible for making decisions about the activities of an organization. Business owners, managers, investors as well as politicians are all examples of this type of decision maker.
 Marketing surveys are useful tools because they can help you gather information to make more informed business decisions. How big is your target market? Will the product you’re considering launching appeal to your current customers? What are the attitudes of your customers about your company or product(s)? Surveys can help you answer these and other questions.
Marketing surveys are useful tools because they can help you gather information to make more informed business decisions. How big is your target market? Will the product you’re considering launching appeal to your current customers? What are the attitudes of your customers about your company or product(s)? Surveys can help you answer these and other questions.